Value investing at its core is the marriage of a contrarian streak and a calculator. Seth Klarman- Hedge Fund Value Investor.
We touched on this subject at the end of April, but thought it might be a good idea to look at the subject of present and future value discounting in more detail.
Last week the Bank of England raised interest rates by 0.25% to 0.75%; although Mortgage rates moved at the speed of light, (I got an e-mail from HSBC telling me that my mortgage was going up 2 and a half hours later!), it appears that savings rates will be moving at a more sedate (or glacial) pace. Many of the newer UK house buyers have not seen a rate rise at all (as we have been stuck at or below 0.5% since 2009), and the effect on consumer spending and confidence is unclear.
What is also unclear is the effect on asset prices – interest rates are a crucial input to the valuation process in both bonds and equities (as well as house prices). This is because they determine the present value of future cash flows that accrue to the holders of the asset in question over time. For bonds, it is relatively easy to understand – as interest rates rise, so bond prices fall, as they need to fall (to raise their yields to compete with the new, higher alternative investments). But for equities, it is a little more complicated, as they have an infinite life (apart from a few unfortunates), which means that one needs to look further into the future – a lot further in fact.
One of the most popular methods to value equities is the Discounted Cash Flow method, whereby cashflows (be it dividends, earnings or share-buyback proceeds) due to arrive in the future are translated into present-day values [1].
The effect of recent Interest rate changes can be seen more clearly via DCF models. Using the 3-year example below, (and further assuming that rates rise equally across the maturity spectrum – see below for the caveats – a 0.25% rise in interest rates would reduce the value of those cash flows to £1/1.0275 + £1/1.0325^2 +£1/ 1.0375^3 = £2.80, a 0.71% drop in intrinsic worth. That may not sound like a lot, but combined with a drop in P/E ratios, which tends to occur when rates rise, can lead to major changes in share prices.
This methodology can be used for Indices as well as individual shares, so let us use the FTSE All Share Index as an example. As of July 2018, the Index is expected to pay out a Dividend of £141.60 this year, which we shall assume grows by 5% per annum indefinitely; this requires a slightly modified version of the DCF, known as the Gordon Growth Model. (The formula is the Intrinsic value of stock = D/(k-g), where D= Dividend, k = required rate of return, which we will assign as 8% and g = dividend growth of 5% in perpetuity).
Thus “fair value” is 141.6/0.08-0.05 = 141.6/0.03 = 4,720, which is above the current value (4,246 as of 07/08/18), suggesting that the Index is “cheap”.
Now, there are a lot of potential pitfalls with this analysis. Both DCF and the GGM are heavily sensitive to the discount rate used and the further out in time one goes, the more difficult to estimate the cash flow it becomes – a dividend of £141.6 in 30 years time is worth only £32.77 at a 5% interest rate (and just £28.41 at a rate of 5.5%), so even small changes in rates have an enlarged effect on long-term cash flows. Changing the required rate of return to 9% (0.09) in the above example, or slowing the rate of dividend growth (g) to 4% p.a. reduces the valuation using the GGM to 3,540 – a substantial drop. We also have to assume that interest rates will actually move in parallel (i.e. the yield curve does not flatten for example), which has not been the case recently and thus may explain why US equities have largely ignored the Fed’s recent hiking programme. It is also the case that interest rates alone are not the only input into the decision to buy and sell. If they were, prices would be considerably less volatile than they are in reality.
There are other problems with this method, which this pdf highlights, but in the absence of compelling alternatives, the investment industry tends to prefer to stick with what they know, with the result that the process becomes more of an art than a science.
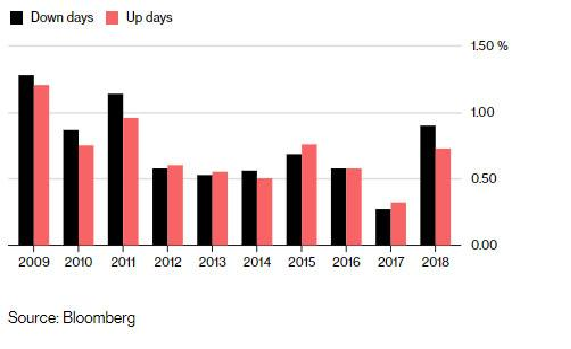
Assuming that Global Interest rates are, or are close to, bottoming, we may see a change in how assets are valued; it is a certainly causing a degree of nervousness amongst equity markets, as shown below. Despite being up 7.7% this year in Dollars (and 13% in Sterling), the S&P 500 has seen more down days than up, with the ratio between the two at the highest levels since 2008. In addition, the total Short interest on the New York Stock Exchange is currently (as of the last reporting period of mid-July) over 13.5 BILLION shares, which as Tesla short sellers will confirm, can lead to an enormous pent-up buying power (as they will have to cover their positions at some point, with potentially huge losses). Paradoxically, this huge level of latent bearishness can provide assurance that markets will not fall far (for long), though that does not preclude bouts of periodic volatility. Indeed, the recent trend of strong gains followed by sudden lurches downwards is exactly what we could expect from this dynamic. But unless you have a penchant for soap operas, it may be better to switch off CNBC/Bloomberg News and concentrate on more productive ways to spend one’s time. Markets are big and ugly enough to look after themselves…
[1] Imagine that you will receive £100 in a year’s time. If interest rates are at 5%, then the value in today’s money is £100/1.05 = £95.24. (Divide the future payment by the interest, or discount rate). Alternatively, £100 today would be worth £100 x 1.05 = £105 in one years time. The basic idea is that money here and now is more valuable than that in the future. The same principle works for dividends/share buybacks and earnings – in order to compare alternatives, they need to be converted into today’s money. Businesses routinely use a form of this to evaluate the worth (or otherwise), of their future ventures – as interest rates rise, the “hurdle rate” (or the minimum return the business needs to make to justify the investment) rises.
The formula is Discounted Value = Cash Flow /Interest Rate; (or like this in mathematical notation), where n is the number of years before the cash flow materialises.
Let us imagine a firm that will pay out £1 per share in Dividends over the next 3 years, and assume one, two and three-year interest rates are 2.5%, 3%, and 3.5% respectively; the DCF Value of these pay-outs would thus be;
£1/1.025 + £1/1.03^2 + £1/1.035^3 = 0.9756+ 0.9426 + 0.902 = £2.82. One would then compare this sum to the market price of the asset being appraised.
(Although this example is stylised, the interest rates used for discounting purposes should be those of Corporate bonds of comparable maturity, rather than UK Government bonds, as the latter has no credit risk; here, we are looking at Corporate cashflows, which of course are risky).